Jag har lagt till DFT och vinklarna till chirpen. Bilderna hämtar jag via Visa_DFT.
chirp_test_basic med utförlig kommatering
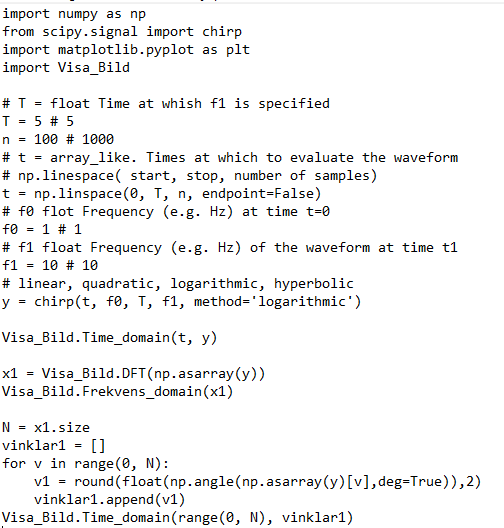
chirp_test_basic senaste versionen
import numpy as
np
from scipy.signal import chirp
import matplotlib.pyplot as plt
import Visa_Bild
import math
# Första delan skapar en chirp.
# Andra delen kör en DFT
# Tredje delen redovisar readel och phase
# SampleRate motsvarar 44100Hz
T = 0.1
n = 4410
t = np.linspace(0, T, n, endpoint=False)
f0 = 5000
f1 = 10000
# linear, quadratic, logarithmic, hyperbolic
y = chirp(t, f0, T, f1, method=’linear’)
Visa_Bild.Visa_Kurva(t, y
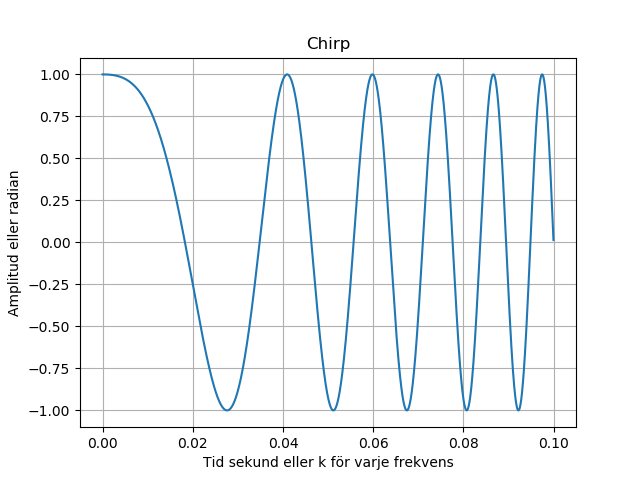
x1 =
Visa_Bild.DFT(np.asarray(y))
x_normed = (x1 – x1.min(0)) / x1.ptp(0) #normaliseras till 1 – -1
Visa_Bild.Visa_Balkar(x1
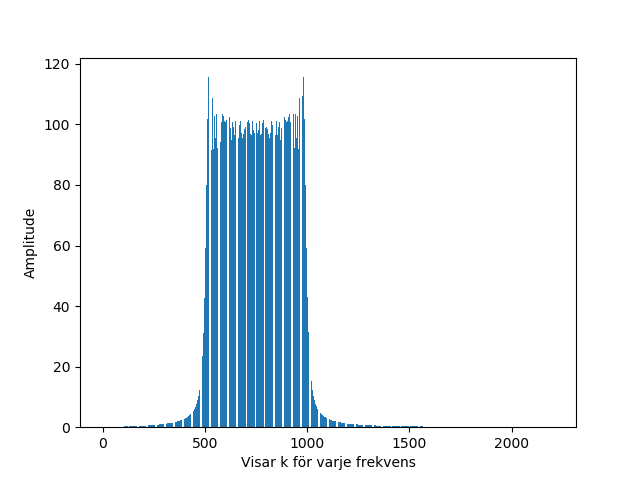
N = x1.size
k_f0 = int((f0*N)/n*.1)
k_f1 = int((f1*N)/n*.1)
bredd = math.floor(N/2)
vinklar1 = []
real = []
for k in range(0, bredd):
v1 =
round(float(np.angle(np.asarray(x1)[k],deg=False)),2)
a1 =
round((np.real(np.asarray(x_normed)[k])), 2)
vinklar1.append(v1)
real.append(a1)
Visa_Bild.Visa_Kurva(range(0, bredd), vinklar1)
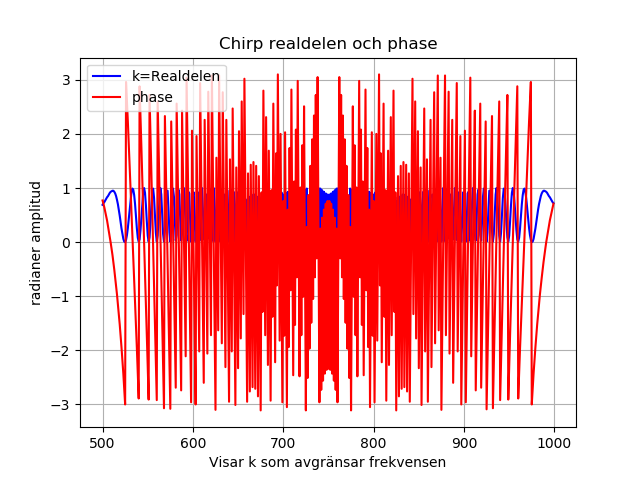
y = vinklar1[k_f0:k_f1]
x = real[k_f0:k_f1]
Visa_Bild.Visa_Flera(x, y, k_f0, k_f1)
Visa_Bild
import
matplotlib.pyplot as plt
import numpy as np
import math
def Visa_Kurva(t,
x):
fig, (ax1) = plt.subplots()
ax1.plot(t, x)
ax1.set(xlabel=’Tid sekund eller k
för varje frekvens’, ylabel=’Amplitud eller radian’, title=’Chirp’)
ax1.grid()
plt.show()
def Visa_Flera(x,
y, k_f0, k_f1):
f = range(k_f0, k_f1)
fig, (ax1) = plt.subplots()
ax1.plot(f, x, ’-b’,
label=’k=Realdelen’)
ax1.plot(f, y, ’-r’,
label=’phase’)
plt.legend(loc=’upper left’)
ax1.set(xlabel=’Visar k som avgränsar
frekvensen’, ylabel=’radianer amplitud’, title=’Chirp realdelen och
phase’)
ax1.grid()
plt.show()
def
Visa_Balkar(x):
N = x.size
bredd = math.floor(N/2)
y = np.absolute(x)[:bredd]
f = np.linspace(0, N, N)
plt.ylabel(”Amplitude”)
plt.xlabel(’Visar k för varje
frekvens’)
plt.bar(f[:N//2], y, width=0.8)
plt.show()
#plt.pause(0.1)
#plt.close()
def DFT(x):
N = x.size
n = np.arange(N)
k = n.reshape((N, 1))
e = np.exp(-2j * np.pi * k * n /
N)
return np.dot(e,x)
Utvärdering
Idag gick det bättre. Nu kan jag jämföra en chirp med avseende på frekvens domain.